Everyone needs to initialize neural net (NN) weights when training NN models. This post describes why we need a good weight init and how to do that.
TLDR:
1. From intuition, good weight initialization provides a good path under the weight landscape.
2. From deduction, good weight initialization keeps activation within a stable range.
Activation is not stable across different layers when you use random initialization
The activation of each layer explodes or shrinks very quickly.
From the above result, after 100 layers, the activation value explodes. More specifically, after 28 layers, it becomes NaN already.
On the other hand, if you initialize weights within a small range, the activation shrinks to 0. All these results indicate activation of each layer needs special consideration. A criterion for good weight initialization is to keep activation suitable: not 0, not too large (presumably always within (0, 1]).
Weight initialization by rescaling based on layer depth
The below schema illustrates the activation of a layer. We can compare the input \(Z^{i-1}\) and output \(Z^{i}\) to see their relationship, as followed:
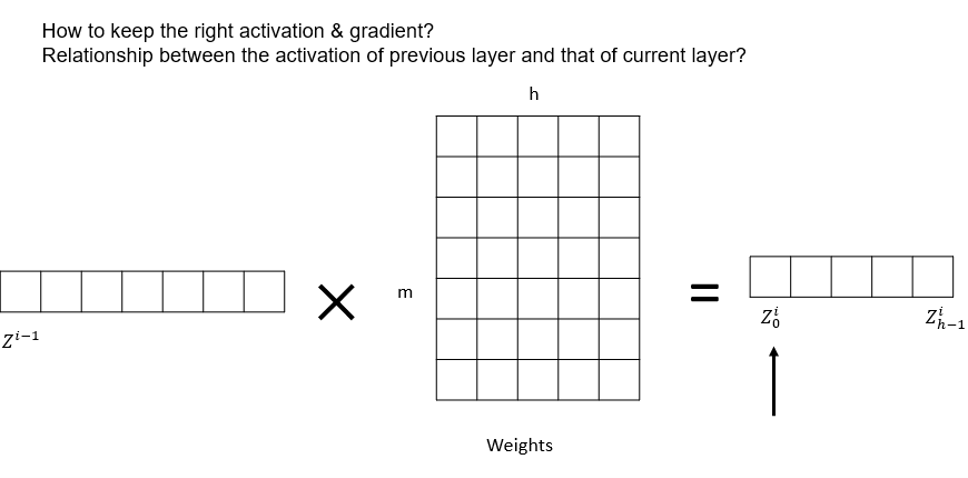
With this schema, we have this formula:
Specifically, the above deduction indicates that (when ignoring activation function's effect) there's \(m\)-fold increase after each layer activation, where \(m\) is the number of neurons in this layer. We can also see this same conclusion from the experiment below, note that output.std() == sqrt(16).
Common weight initialization: Xavier and He
Researchers have had this same finding and have proposed tips for a good weight initialization. When taking activation function into account, Xavier Init is more suitable for NN with TanH activation while He Init is more suitable for NN with ReLU activation (which is what this post is based on).
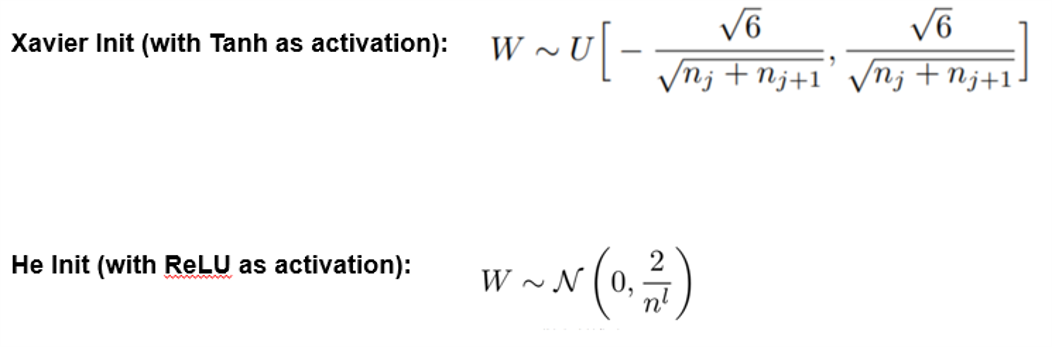
Experimental validation
This section creates a simple NN with ReLU activation, and did experiments to validate that He Init can help stablize NN activation. First, we check, with He Init, whether activation is stable after one layer.
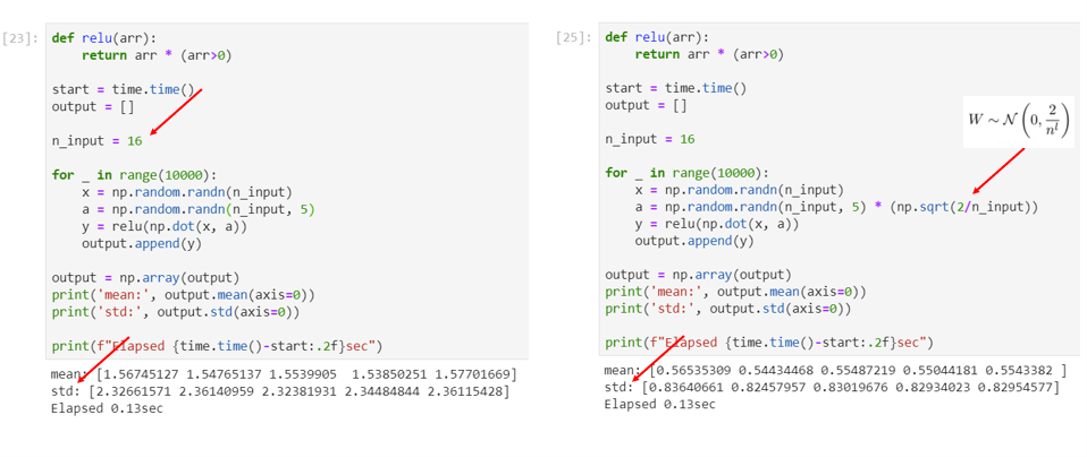
The above results shows that, once we re-scale the weight with 2/sqrt(N), the activation becomes stable (for one iteration, one layer). If we rescale the weights by each layer, we can see activation is stabilized across multiple layers, and is agnostic to the number of inputs, as below:
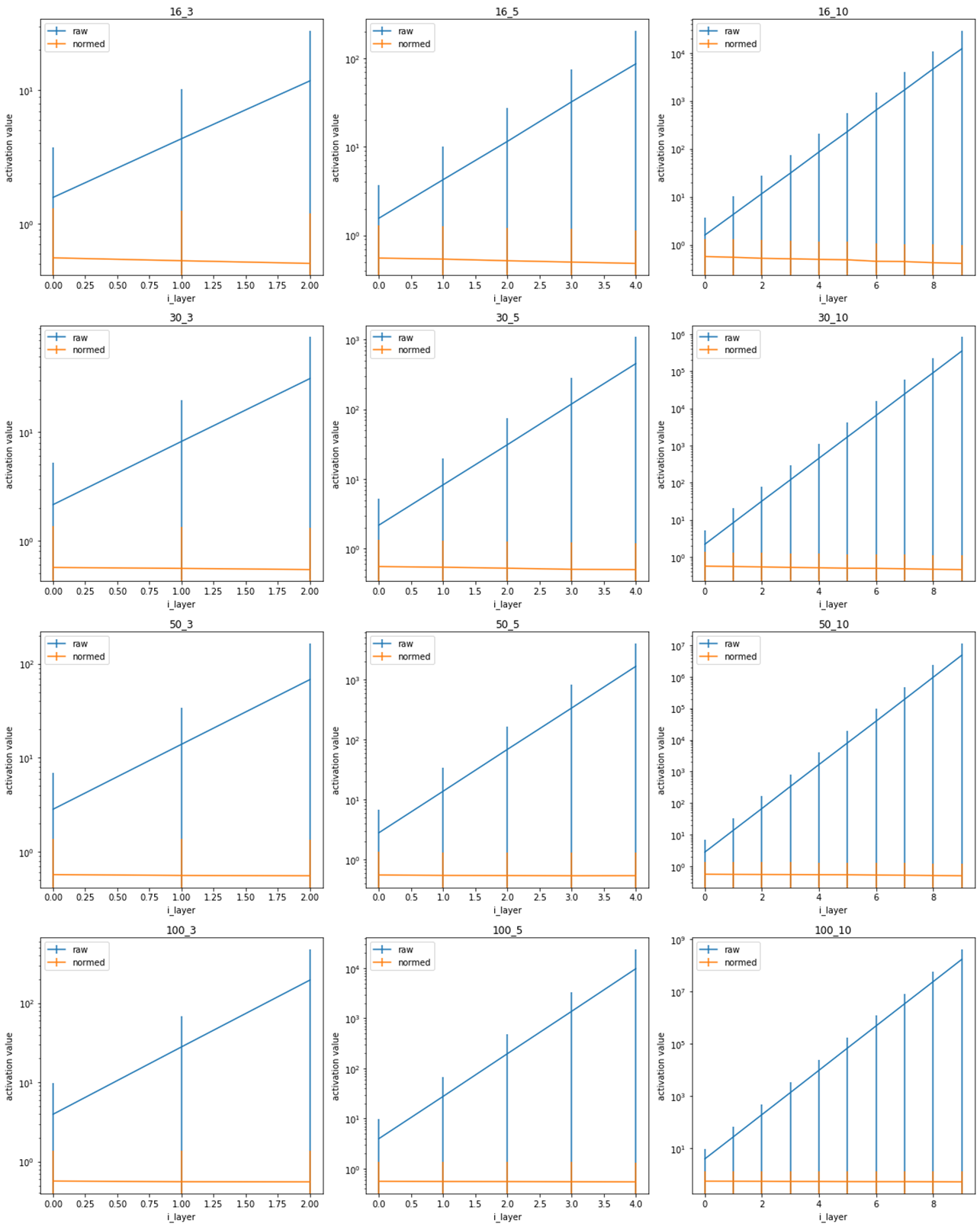Legend: x-axis represents the index of layer in the NN; y-axis represents the averaged mean of weights; error bar represents the averaged standard deviation of weights in a specific layer; title m_n indicates that the NN has m input_neurons at each layer and there are n layers; experiments are repeated 1000 times.
In the above results, the blue curve (activation distribution of NN with randomly initilized weights) explode very quickly in the deeper layers, while the yellow curve (with He Init on each layer) remains stable. All the above proves that when weight initiation is done correctly, the NN activation can stay stable across different layers.
Conclusions and learning
- We have theoretical and experimental results supporting the importance of a good weight initialization.
- It will be helpful to monitor stats of each layer to diagnose training process
- The weight scaling seems to have nothing to do with NN depth, i.e. we can stabilize the whole NN simply via stabilizing each individual layer independently.
- This raises a follow up question: can we use an optimizer to find the best weight initialization for any NN config? Also, if we have normalization layers, do we still need weight init tricks?
Refs:
Comments